Tópico 13
Matrizes Definidas Positivas

Pedro Aladar Tonelli

Matrizes Simétricas

Uma matriz $A\in \mathbb{R}^{n\times n}$ é simétrica se $A=A^T$

Propriedades:

  • Os autovalores são todos reais
  • Tem $n$ autovetores ortogonais
  • $A= G^T \Lambda G$ (teorema espectral)
  • $A = LDL^T$ (Cholesky)

Matrizes Positivas

Uma matriz simétrica $A$ é definida positiva quando \begin{gather} \langle x,Ax \rangle > 0 \forall x \neq 0 \\ \langle x,y \rangle = \sum_{i=1}^n x_iy_i \end{gather}

Exemplos

\begin{gather} A_1 = \begin{bmatrix} 1 & 2 \\ 2 & 1 \end{bmatrix}\text{ } A_2 =\begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} \\ A_3 = \begin{bmatrix} -1 & 2 \\ 2 & 10 \end{bmatrix}\text{ } A_4=\begin{bmatrix} a & b \\ b & c \end{bmatrix} \end{gather}

Teorema

São equivalentes:

  1. $\langle x,Ax \rangle > 0 \forall x \neq 0$
  2. Todos os autovalores de $A$ são positivos
  3. $\operatorname{det}(A_k)>0$ com $A_k =A[1:k,1:k]$
  4. Os pivôs da matriz $D$ na decomposição de Cholesky são positivos.

Exemplo importante

Se $B$ é uma matriz quadrada qualquer então $A=BB^T$ é semi-definida positiva, isto é

$$ \langle x,Ax \rangle \geq 0 \forall x \neq 0$$ $A$ pode não ser invertível

Outro Teorema

Uma matriz simétrica $A$ é definida positiva se e somente se existe uma matriz $R$ com $n$ colunas LI (posto $n$) tal que $$ A = R^TR $$

Formas quadráticas

Se $A$ é uma matriz simétrica então a função $f_A: \mathbb{R}^n \to \mathbb{R}$ definida por $f_A(x)=\langle x,Ax \rangle$ é uma forma quadrática. Se $A$ é definida positiva, a forma quadrática também é dita definida positiva.

Otimização

Se $f:\mathbb{R}^2 \to \mathbb{R}$ é uma função diferenciável na origem. Então seu desenvolvimento em série de Taylor em torno da origem começa com: \begin{gather} f(x,y)= f(0,0) + x\frac{\partial f}{\partial x}(0,0)x + \frac{\partial f}{\partial y}(0,0)y + \\ \frac{1}{2!}\left(\frac{\partial^2 f}{\partial x^2}(0,0)x^2 +\frac{\partial^2 f}{\partial y^2}(0,0)y^2 + \frac{\partial^2 f}{\partial x \partial y}(0,0)xy\right) + \dots \end{gather}

Elipsoides

No caso de uma matriz definida $A$ positiva o conjunto $$ \mathcal{E} = \{ x\in \mathbb{R}^n : f_A(x) =1\} $$ define um Elipsoide com os eixos principais coincidindo com as direções dos autovetores, e $\frac{1}{\sqrt{\lambda_i}}$ os raios do elipsoide na direção do correspondente eixo.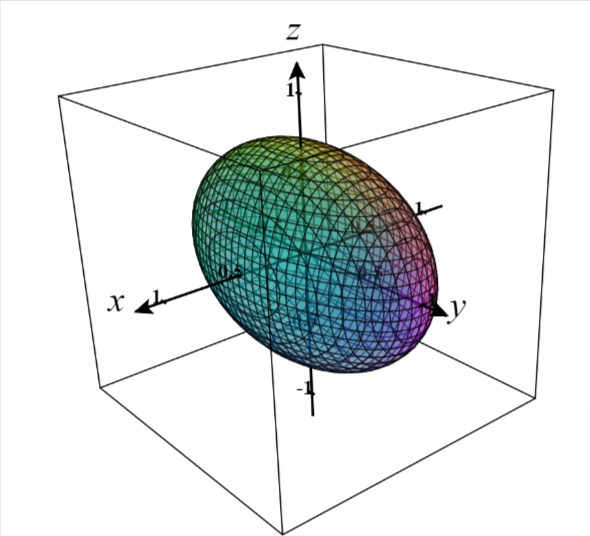
Figuras feitas no C3D

Relação de congruência

Diremos que duas matrizes simétricas, $A_1$ e $A_2$ são congruentes, quando existir uma matriz invertível $P$ tal que $$ A_2 = P^TA_1P$$ Note que elas não precisam ser semelhantes.

Exemplos

\begin{gather} A=\begin{bmatrix}1 & 0 \\ 0 & 0 \end{bmatrix}\text{ } B= \begin{bmatrix}-1 & 0 \\ 0 & 0 \end{bmatrix} \\ C=\begin{bmatrix}2 & 0 \\ 0 & 1 \end{bmatrix}\text{ }D=\begin{bmatrix}1 & 0 \\ 0 & 1 \end{bmatrix} \end{gather}
Se $A$ é uma matriz simétrica, e $A=G^T\Lambda G$ é uma decomposição espectral
  • O número de autovalores positivos de $A$, chamaremos de índice ($p$)
  • Assinatura de $A$ é o número de autovalores positivos menos os negativos ($p-n$)
  • O posto de $A$ é $r$

Teorema da inércia de Sylvester

$A$ e $B$ são matrizes congruentes se, e somente se, possuem o mesmo índice $p$ a mesma assinatura $a$ e o mesmo posto $r$