Tópico 3
Projeções ortogonais e MMQ

Pedro Aladar Tonelli

Vetores ortogonais

Vamos considerar um espaço vetorial $V$ com um produto interno $\langle \cdot , \cdot \rangle$. Dizemos que dois vetores $\vec{x}$ e $\vec{y}$ são ortogonais quando $\langle \vec{x}, \vec{y} \rangle =0$. Uma família de vetores $\{ \vec{x_1},\dots,\vec{x_n} \}$ é ortogonal quando são dois a dois ortogonais. Uma tal família é sempre LI.

Base ortonormal

$\{\vec{e_1}, \dots, \vec{e_n} \}$ base ortogonal se é base e se for ortogonal. diremos que esta base é ortonormal quando $$\langle \vec{e_i},\vec{e_j} \rangle = \delta_{ij}$$ Em qualquer subespaço $W \subset V$ podemos tomar uma base ortogonal deste subespaço.

Complemento ortogonal de um subespaço

Se $W \subset V$ é um subespaço vetorial de $V$, podemos definir o complemento ortogonal como \[ W^{\bot}=\{\vec{y}\in V: \langle \vec{y},\vec{x}\rangle =0 \quad \forall \vec{x} \in W \}\]

Projeção ortogonal

Se $W \subset V$ é um subespaço vetorial de $V$. Tomamos uma base ortogonal em $W$:$\{ \vec{f_1} ,\dots, \vec{f_k} \}$ e definimos a aplicação $ \Pi: V \to $ como \[ \Pi( \vec{x}) = \sum_{i=1}^k \frac{\langle \vec{x}, \vec{f}_i \rangle}{\langle \vec{f}_i,\vec{f}_i\rangle}\vec{f}_i\]

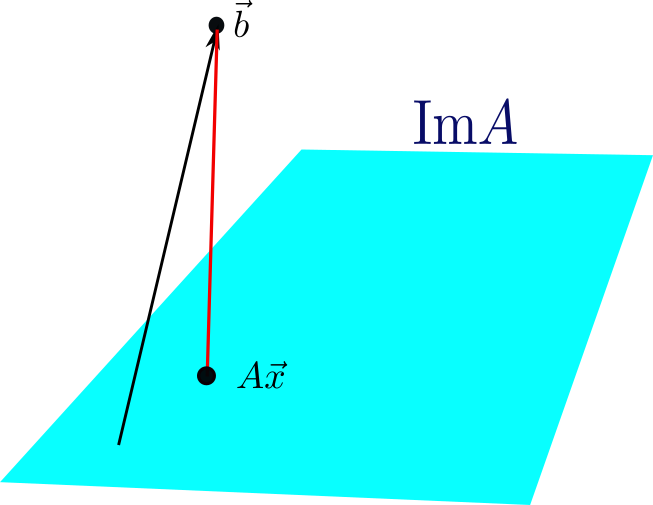
Problema MMQ

Suponha que $A$ seja uma matriz $n\times k$ de posto $k$ e com $k< n$. Então Im$A$ é um subespaço de dimensão $k$ em $\mathbb{R}^n$. O sistema linear: \[ A\vec{x} = \vec{b}\] só terá uma solução se $\vec{b}\in \text{Im}A$ caso contrário não haverá solução e podemos definir a solução por MMQ como aquela que minimize o resíduo $\| A\vec{x}-\vec{b}\|^2$

A solução do MMQ

Temos que encontrar um vetor $\vec{x}$ tal que $\vec{b} - A\vec{x}$ seja ortogonal ao espaço $\text{Im}A$, ou seja: $$ \begin{gather*} \langle \vec{b} - A\vec{x} , A\vec{y} \rangle = 0 \quad \forall \vec{y} \in \mathbb{R}^n \\ \langle A^T(\vec{b} - A\vec{x}) , \vec{y} \rangle = 0 \quad \forall \vec{y} \in \mathbb{R}^n \\ A^T\vec{b} - A^T A\vec{x} =0 \text{ ou }\\ A^T\vec{b} = A^T A\vec{x} \end{gather*} $$