Tópico 2
Decomposição LU
Pedro Aladar Tonelli
Algoritmo da eliminação de Gauss
Este Algoritmo é um método de escalonamento de uma matriz $M$ de dimensão $m\times n$.
Se $\mu = \min\{m,n\}$ Então executamos de $k=1$ até $\mu-1$ os passos seguintes
descrição do passo $k$
- Se $a_{kk}=0$ troca a linha $k$ com uma linha $i>k$ tal que $a_{ik} \neq 0$
- da linha $k+1$ até $m$ fazemos $L_i = L_i - \nu_{ik}L_k$ onde $\nu_{ik}=\frac{a_{ik}}{a_{kk}}$
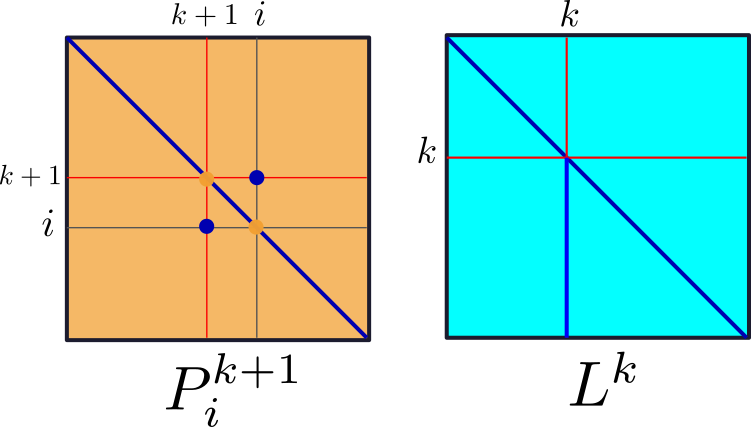
Ilustração
O algoritmo usando Matrizes elementares
A operação que troca a linha $k$ e $i$ chamaremos de $P^k_i$
\[ P^k_i =
\begin{array}{c|ccccc|}
& &k & \cdots& i & \\ \hline
& I & 0 & 0 & 0 & 0\\
k & 0 & 0 & 0 & 1 & 0\\
\vdots & 0 & 0 & I & 0 & 0\\
i & 0 & 1 & 0 & 0 & 0\\
& 0 & 0 & 0 & 0 & I\\ \hline
\end{array}\]
Depois devemos executar as operações que denotamos
$$ L_i= L_i-\mu_{ik}L_k = L^k_i$$
Estas operações afetam apenas a $i$-ésima linha da matriz e devemos executá-las
para $i\in \{k+1,\dots, m\}$
Vamos denotar $L^k= L^k_m \cdots L^k_{k+1}$
A matriz de $L^k$
\[ L^k =
\begin{array}{c|ccccc|}
& &k & \cdots& & \\ \hline
& I & 0 & 0 & 0 & 0\\
k & 0 & 1 & 0 & 0 & 0\\
& 0 & -\mu_{{k+1}k} & 1 & 0 & 0\\
& 0 & \vdots & 0 & \ddots & 0\\
& 0 & -\mu_{mk} & 0 & 0 & 1\\ \hline
\end{array}\]
O escalonamento da matriz $M$ segue-se então executando na ordem o
seguinte produto de Matrizes
$L^{m-1}P^{m-1}_{i_{m-1}} \cdots $ $L^k P^k_{i_k}$$\cdots$ ${L^1P^1_{i_1}}$ $M$
onde $i_k \geq k$
Exemplo
\[ M= \begin{pmatrix} 2 & 3 & 1 \\
4 & 5 & 3 \\
2 & 5 & 1 \end{pmatrix}\]
\[ L^1 = \begin{pmatrix} 1 & 0 & 0 \\
-2 & 1 & 0 \\
-1 & 0 & 1 \end{pmatrix}\]
\[ L^1 M= \begin{pmatrix} 2 & 3 & 1 \\
0 & -1 & 1 \\
0 & 2 & 0 \end{pmatrix}\]
\[ L^2 = \begin{pmatrix} 1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 2 & 1 \end{pmatrix}\]
\[ L^2 L^1 M= \begin{pmatrix} 2 & 3 & 1 \\
0 & -1 & 1 \\
0 & 0 & 2 \end{pmatrix}\] ou
\[ M = (L^1)^{-1}(L^2)^{-1} \begin{pmatrix} 2 & 3 & 1 \\
0 & -1 & 1 \\
0 & 0 & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\
2 & 1 & 0 \\
1 & -2 & 1 \end{pmatrix}\begin{pmatrix} 2 & 3 & 1 \\
0 & -1 & 1 \\
0 & 0 & 2 \end{pmatrix}\]
Definição: Dizemos que uma matriz quadrada de dimensão m, $L=(l_{ij})$
é triangular inferior (ou do tipo L) quando
- $l_{ii}=1$
- $l_{ij}=0$ se $i\lt j$
Definição: Dizemos que uma matriz quadrada de dimensão m, $U=(u_{ij})$
é triangular superior (ou do tipo U ) quando $u_{ij}=0$ se
$i \gt j$
Teorema: Toda matriz quadrada pode ser decomposta como
o produto $M = PLU$ ou equivalentemente em $PM = LU$
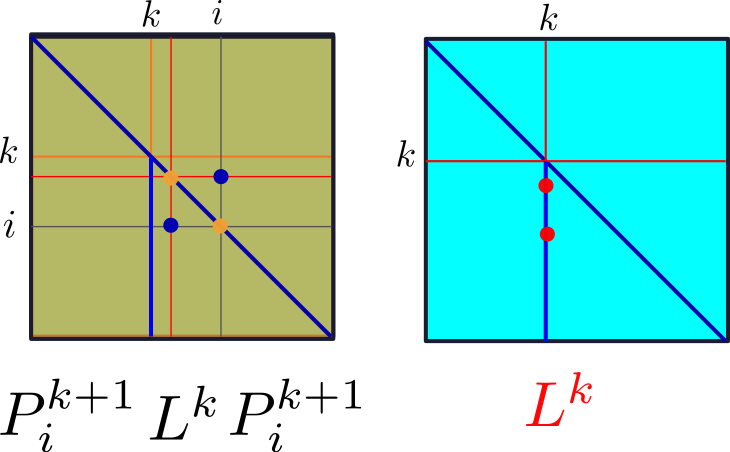
Vamos ver como fica o caso geral:
$L^{m-1}P^{m-1}_i\cdots$ $P^{k+1}_iL^kP^k_i$ $\cdots P^2_i L^1 P^1_i$
Lema:
$P^{k+1}_iL^kP^k_i=L^k_*P^{k+1}_iP^k_i$
prova:
$P^{k+1}_iL^kP^k_i =$ $P^{k+1}_iL^k I P^k_i$
$P^{k+1}_iL^k$ $P^{k+1}_iP^{k+1}_i$ $P^k_i$
Exemplo
$$
\left[ \begin{array}{cccc}
1 & 1 & -1 & 2 \\
2 & 0 & 1 &1 \\
3 & 1 & 0 & 3 \\
1 & -1 & 0 & 1
\end{array}\right]
$$
$$
\begin{equation}
L_1=\left[
\begin{array}{cccc}
1.0 & 0.0 & 0.0 & 0.0 \\
-2.0 & 1.0 & 0.0 & 0.0 \\
-3.0 & 0.0 & 1.0 & 0.0 \\
-1.0 & 0.0 & 0.0 & 1.0 \\
\end{array}
\right]
\end{equation} $$
\begin{equation}
L_1A=
\left[
\begin{array}{cccc}
1.0 & 1.0 & -1.0 & 2.0 \\
0.0 & -2.0 & 3.0 & -3.0 \\
0.0 & -2.0 & 3.0 & -3.0 \\
0.0 & -2.0 & 1.0 & -1.0 \\
\end{array}
\right]
\end{equation}
$$
\begin{equation}
L_2=\left[
\begin{array}{cccc}
1.0 & 0.0 & 0.0 & 0.0 \\
0.0 & 1.0 & 0.0 & 0.0 \\
0.0 & -1.0 & 1.0 & 0.0 \\
0.0 & -1.0 & 0.0 & 1.0 \\
\end{array}
\right]
\end{equation}
$$
$$
\begin{equation}
L_2L_1A=
\left[
\begin{array}{cccc}
1.0 & 1.0 & -1.0 & 2.0 \\
0.0 & -2.0 & 3.0 & -3.0 \\
0.0 & 0.0 & 0.0 & 0.0 \\
0.0 & 0.0 & -2.0 & 2.0 \\
\end{array}
\right]
\end{equation}$$
$$
\begin{equation}P_3=
\left[
\begin{array}{cccc}
1.0 & 0.0 & 0.0 & 0.0 \\
0.0 & 1.0 & 0.0 & 0.0 \\
0.0 & 0.0 & 0.0 & 1.0 \\
0.0 & 0.0 & 1.0 & 0.0 \\
\end{array}
\right]
\end{equation}
$$
$$
\begin{equation}
U=P_3L_2L_1 =
\left[
\begin{array}{cccc}
1.0 & 1.0 & -1.0 & 2.0 \\
0.0 & -2.0 & 3.0 & -3.0 \\
0.0 & 0.0 & -2.0 & 2.0 \\
0.0 & 0.0 & 0.0 & 0.0 \\
\end{array}
\right]
\end{equation}$$
$$
\begin{gather}
P_3L_2L_1=P_3L_2{(P_3P_3)}L_1(P_3P_3) = \\
(P_3L_2P_3)(P_3L_1P_3)P_3 =
L_2^\prime L_1^\prime P_3
\end{gather}
$$
$$
\begin{equation}L_1^\prime = P_3L_1P_3=
\left[
\begin{array}{cccc}
1.0 & 0.0 & 0.0 & 0.0 \\
-2.0 & 1.0 & 0.0 & 0.0 \\
-1.0 & 0.0 & 1.0 & 0.0 \\
-3.0 & 0.0 & 0.0 & 1.0 \\
\end{array}
\right]
\end{equation}$$
$$
\begin{equation}L_2^\prime L_1^\prime =
\left[
\begin{array}{cccc}
1.0 & 0.0 & 0.0 & 0.0 \\
-2.0 & 1.0 & 0.0 & 0.0 \\
1.0 & -1.0 & 1.0 & 0.0 \\
-1.0 & -1.0 & 0.0 & 1.0 \\
\end{array}
\right]
\end{equation}$$
$$ \begin{equation}L=(L_2^\prime * L_1^\prime)^{-1}=
\left[
\begin{array}{cccc}
1.0 & 0.0 & 0.0 & 0.0 \\
2.0 & 1.0 & 0.0 & 0.0 \\
1.0 & 1.0 & 1.0 & 0.0 \\
3.0 & 1.0 & 0.0 & 1.0 \\
\end{array}
\right]
\end{equation}$$
\begin{equation}
\left[
\begin{array}{cccc}
1.0 & 0.0 & 0.0 & 0.0 \\
0.0 & 1.0 & 0.0 & 0.0 \\
0.0 & 0.0 & 0.0 & 1.0 \\
0.0 & 0.0 & 1.0 & 0.0 \\
\end{array}
\right]
\left[
\begin{array}{cccc}
1 & 1 & -1 & 2 \\
2 & 0 & 1 & 1 \\
3 & 1 & 0 & 3 \\
1 & -1 & 0 & 1 \\
\end{array}
\right]= \\
\left[
\begin{array}{cccc}
1.0 & 0.0 & 0.0 & 0.0 \\
2.0 & 1.0 & 0.0 & 0.0 \\
1.0 & 1.0 & 1.0 & 0.0 \\
3.0 & 1.0 & 0.0 & 1.0 \\
\end{array}
\right]\left[
\begin{array}{cccc}
1.0 & 1.0 & -1.0 & 2.0 \\
0.0 & -2.0 & 3.0 & -3.0 \\
0.0 & 0.0 & -2.0 & 2.0 \\
0.0 & 0.0 & 0.0 & 0.0 \\
\end{array}
\right]
\end{equation}