reveal.js

Tópico 1
Matrizes de Transformações Lineares

Pedro Aladar Tonelli

Matrizes como Transformações Lineares

Vamos relembrar alguns conceitos:

$V$ é um espaço vetorial de dimensão $n$
$\{ e_1, \cdots , e_n\}$ é uma base de $V$
$W$ é um espaço vetorial de dimensão $m$
$\{ f_1, \cdots , f_m\}$ é uma base de $W$
$T$ éum operador linear de $V$ em $W$

Matriz de $T$

$T(e_j) = \sum_{i=1}^m a_{ij}f_i$ A matriz

$A=(a_{ij})$ é a matriz que representa a transformação

$T$ nas bases dadas.

Esquema para memorizar

$\begin{array}{c|ccc|} & T(e_1) & \cdots & T(e_n) \\ \hline f_1 & a_{11} & \cdots & a_{1n} \\ \vdots & & & \\ f_m & a_{m1} & \cdots & a_{mn} \\ \hline \end{array}$

Exemplo

$T: \mathbb{R}^3 \to \mathbb{R}^3$ satisfaz:

$T(2e_1 + e_2) = e_3$

$T(e_1 - e_2) = 2e_3-6e_2$

$T(e_3) + T(e_2)=e_1$

Qual a matriz de

$T$ na base

$\{e_1,e_2,e_3\}$ ?

Operador aplicado a um vetor

Vamos tomar um vetor genérico

$\mathbf{v} = \sum_{i=1}^n x_i e_1$ e calcular

$T(\mathbf{v})$ usando a matriz de representação de

$T$ .

$T(\mathbf{v}) = \sum_{i=1}^n x_iT(e_i) = \sum_{i=1}^n x_i\begin{bmatrix} a_{1i} \\ \vdots \\ a_{mi}\end{bmatrix} = A\mathbf{x}$

Mudança de base

$\begin{array}{ccc} V & \stackrel{T}{\rightarrow} & W \\ \{e_1,\dots,e_n\} & A & \{f_1,\dots, f_m\} \\ \{e^\prime_1,\dots,e^\prime_n\} & A^\prime & \{f^\prime_1,\dots, f^\prime_m\} \end{array}$ Qual a relação entre

$A$ e

$A^\prime$ ?

No espaço vetorial

$V$ temos

$e_j = \sum_{i=1}^n p_{ij} e^\prime_i$ e analogamente no espaço

$W$

$f_j = \sum_{i=1}^m q_{ij} f^\prime_i$

$V$ , se temos um vetor

$\mathbf{v}=\sum_{r=1}^n x_re_r = \sum_{l=1}^n y_le^\prime_l$ Podemos comparar as coordenadas

$\mathbf{x}$ e

$\mathbf{y}$ em duas bases diferentes da seguinte forma:

$\mathbf{v}=\sum_{r=1}^n x_re_r =\sum_{r=1}^n x_r(\sum_{i=1}^n p_{ir} e^\prime_i)$ reagrupando as somas temos:

$\mathbf{v}=\sum_{r=1}^n x_re_r =\sum_{i=1}^n (\sum_{r=1}^n p_{ir} x_r) e^\prime_i)$ ou

$y_i = (\sum_{r=1}^n p_{ir} x_r) \implies \mathbf{y}=P\mathbf{x}$

Analogamente no espaço

$W$ , se as coordenadas de um vetor nas diferentes bases

$\begin{bmatrix} w_1 \\ \vdots \\ w_m \end{bmatrix} \text{ na base } f \text{ e } \begin{bmatrix} u_1 \\ \vdots \\ u_m\end{bmatrix} \text{ em } f^\prime$ então

$\mathbf{u} = Q \mathbf{w}$

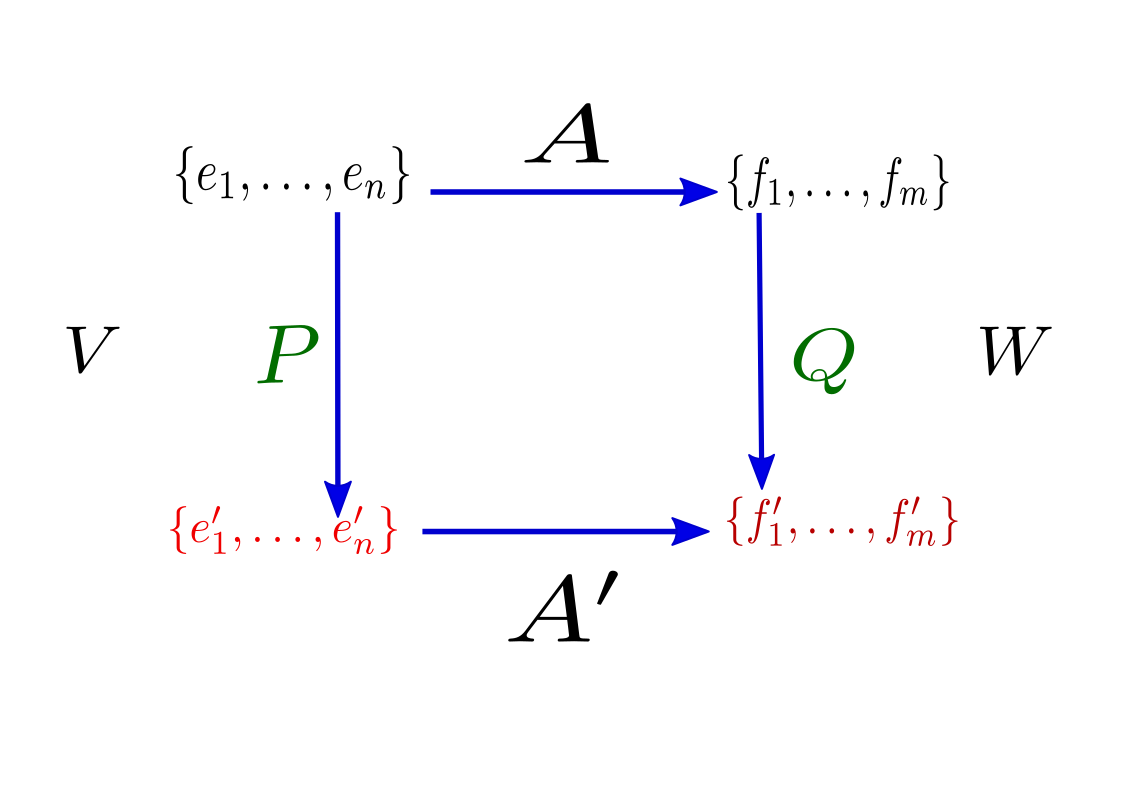
Tópico 1 Matrizes de Transformações Lineares

Pedro Aladar Tonelli

Tópico 1
Matrizes de Transformações Lineares